Hyperraum, Hypermaterie und Reaktoren in Star Wars

[McWire]

Mit diesem visuellen Effekt bin ich nicht ganz einverstanden. Mittelpunkte (sprich Koordinaten) haben nur in UNSERER Welt eine feste mathematische Gültigkeit.
Daher wäre mir das zu einfach.
Wenn z.B. ein dreidimensionaler Würfel in den 4D-Raum "gezogen" wird (und wieder zurück"gequetscht" wird), dann verformt er sich.
Warum nicht so:

http://i1.fastup.de/view.asp?file=8-cell-simple.gif

Nehmen wir doch mal unsere Welt als ein in sich geschlossener 3D-Raum an und weiterhin eine Kugel, als ein in sich geschlossener 4D-Raum.
Beide Räume sind durch den Hyperraum von einander getrennt.
Nun bewegt sich die Kugel (im Hyperraum) entlang einer Achse auf eine bestimmte Koordinate im 3D-Raum zu. Der Vorstellung wegen liegt diese Koordinate "auf der Grenze" der Raumzeit des 3D-Raumes:

http://666kb.com/i/b54ywg2qhtyvy3xol.png

(schwarz=Hyperraum; rot=Bewegungsrichtung der Kugel auf einer Achse im Hyperraum.
Die Raumzeit und der 3D-Raum haben die gleichen Abmessungen. Die Zeit der Kugel hingegen ist bis "unendlich" ausgedehnt, weshalb sie nun auch größer dargestellt ist als der zeitlich begrenzte 3D-Raum)

Ich denke nicht, daß sich die Kugel (im 3D-Raum) von ihrem eigenen "Mittelpunkt" aus langsam nach außen hin "ausdehnt". DENN......sie hatte im Hyperraum keinen Anspruch auf einen einzigen Mittelpunkt - so wie er im 3D-Raum existiert. Im Hyperraum hat sie KEINEN wirklichen Mittelpunkt, denn jeder Punkt der Kugel ist gleichzeitig auch ihr Mittelpunkt. Sprich der "Mittelpunkt" klappt sich um die Außenhülle und die Außenhülle wird zum "Mittelpunkt" (siehe die Animation vom Würfel: das Innere wendet sich nach außen).

Theorie 1
Stößt nun das Gebilde, von dem wir annehmen daß es eine Kugel ist, auf der "Zeit-Achse" mit dem 3D-Raum zusammen, so wird im 3D-Raum m.E. zuerst das sichtbar was "zuerst ankommt":

http://666kb.com/i/b54xzxsb8p05euro2.png

(schwarz=Hyperraum; rote Linie=Bewegungsrichtung auf einer Achse; gelb=Grenze zwischen Hyperraum und Raum-Zeit.)
Allerdings können wir - die wir im 3D-Raum sind - nicht vorhersagen, welche Punkte der Kugel zuerst unsere Raum-Zeit durchdringen. Es könnte der Mittelpunkt sein, es könnte aber auch jeder andere Punkt sein.
Somit könnte sich die Kugel im 3D-Raum, von absoluter Transparenz bis zur völligen Undurchsichtigkeit materialisieren, um kurz darauf genau so spektakulär wieder zu verschwinden. Oder aber es schaffen immer einige wenige Punkte der Kugel gleichzeitig in unseren 3D-Raum, und die Kugel hat ab dem Zeitpunkt wo sie "auftaucht" bis zu dem Zeitpunkt wo sie "verschwindet" gleichbleibende Transparenz.

Theorie 2
Natürlich kann man auch annehmen dass jeder Punkt der Kugel gleichzeitig (aus dem Hyperraum) in den 3D-Raum "eindringt" - da die "Grenze" ledeiglich die ZEIT ist (und nicht irgend eine Wand).
Es würde "Peng" machen und die Kugel wäre materialisiert. Das würde nur eine Millisekunde dauern oder noch kürzer. Verdammt schnell eben.^^
Also zuerst wäre nichts weiter zu sehen als der Sternenhimmel und "im nächsten Agenblick" würde da eine Kugel mit 160km Durchmesser "schweben": Der Todesstern.


Bei aller Thorie glaube ich jedenfalls nicht, daß wir einfach von der Problematik "3D-Körper durchdringt 2D-Körper" auf unser Problem mit der 4D-Kugel schließen können, und einfach annehmen dürfen, der selben Effekt wie in der Flächenwelt träfe nun auch auf die 3D-Welt zu, wenn diese von einer 4D-Kugel gurchdrungen wird.
Das wäre m.E. zu einfach. Und irgendwie auch langweilig.

Meine visuelle Darstellung trifft aber nunmal zu und lässt sich sogar mathematisch beweisen, da Kreis, Kugel und Hyperkugel nur jeweils eine Drehfigur des jeweils niedrigdimensionaleren Gegenstück ist.
Im übrigen gibt es in der Geometrie keine Zeit, alle Dinge sind statisch.
Unsere gedachte Bewegung ist im Prinzip nur die Abfolge der (n-1)-dimensionalen Schnittbilder des n-dimensionalen Objektes, sonst nix weiter.

Eine Hyperkugel hätte genau wie eine Kugel oder ein Kreis nur einen Mittelpunkt.
Ein Kreis ist eine zweidimensionale symmetrisch gekrümmte Begrenzung, eine Kugel ist eine dreidimensionale symmetrisch gekrümmte Begrenzung und eine Hyperkugel ist eine vierdimensionale symmetrisch gekrümmte Begrenzung.

Eine Kugel entsteht, wenn ich einen Kreisen um einer seiner beiden radialen 2D-Achsen drehe, eine Hyperkugel entstünde, wenn ich eine Kugel um einer ihrer radialen 3D-Achsen drehen würde.
Eine fünfdimensionale Hyperhyperkugel würde entstehe, wenn ich eine Hyperkugel um eine ihrer radialen 4D-Achsen drehen würde.

Betrachten wir zunächst mal was passiert, wenn eine Kugel durch eine zweidimensionale Ebene durchwandert.:

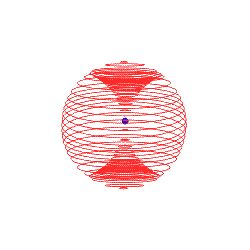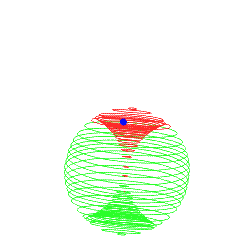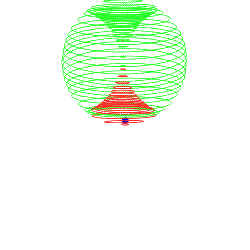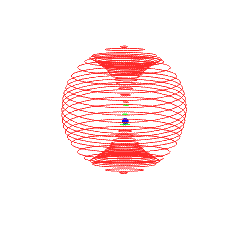
Im Prinzip kann man sich das schnell bildlich erklären, indem man eine Kugel in Schnittbilder zerlegt.
Die Schnittbilder wären allesamt Kreise, bis auf die beiden Pole, die wären Punkte.
Wenn eine Kugel senkrecht in die 2D-Ebene eindringt, würde man zunächst einen Punkt sehen, der dann in Kreise übergeht, welche im Radius wachsen, bis die Kugel ihren Äquator erreicht hätte und anschließen würden die Kreise wieder kleiner werden. Irgendwann kommt der Gegenpol in Form eines Punktes und dannach wäre die Kugel wieder vollständig ausserhalb der Ebene.

Wenn man nun den Winkel variiert, so würden die entstehenden Kreise eine Vorwärtsbewegung erfahren. Wenn man die Geschwindigkeit variiert, würde der Vorgang einfach schneller oder langsamer ablaufen, aber an der Reihenfolge würde sich nix ändern.

Bei einer Hyperkugel durch eine 3D-"Ebene", wäre es im Prinzip genau das gleiche, nur das statt Kreise eben eine Kugel entstünde, die ja nix weiter als ein 3-dimensionale Kreisrotation darstellt.

Das schöne bei einer Kugel oder Hyperkugel ist ja deren Spiegel- und Achsensymmetrie, sodass die Abfolge immer gleich ist, egal mit welcher "Seite" sie zuerst durchbricht.

Bei einem Würfel ist das schon komplizierter, da dort entscheident ist, ob er senkrecht zu einer der Flächen, mit einer Kante vorran, mit einer Ecke vorran oder eine Kombination davon durchbricht... jedesmal ergäbe sich ein anderer Ablauf. Bei einer Kugel oder Hyperkugel ist es immer identisch.

[arthur]

Ja, mir sind diese Modelle bekannt:
Wiki.
Mir leuchtet auch deine Logik ein.

In der Geometrie hast du damit sicher recht:
Natürlich sind es Kreise die eine Kugel in einer Flächenwelt formt (beginnend und endend mit einem Punkt). Was der Flächenweltbewohner wahrnimmt sind die Umfänge der Kreise - welche der Schatten der Kugel sind. Richtig?

Aber WARUM sollte der Betrachter aus der 3D-Welt NUR die Oberflächen der 3D-Kugel sehen - welche der Schatten der 4D-Kugel sind - die sich langsam zur maximalen Größe ausdehnen, OHNE die sich (möglicher Weise) verändernde Position des Kugel-Mittelpunktes im Raum?
Und WENN sich dieser Mittelpunkt - da er aus dem Hyperraum kommt - Z.B. in einer 1/1000 Sekunde von einem weit entfernten Ort (im 3D-Raum), plötzlich in Sichtweite des Betrachter bewegt, DANN sieht der Betrachter doch zwangsläufig - Peng - eine Kugel die "einen Augenblick zuvor" noch nicht da war.

Außerdem trifft das mit den sich ausdehnenden Oberflächen, doch NUR auf eine reine geometrische Kugel (im wahrsten Sinne des Wortes) zu.
Oder sieht man z.B. beim Todesstern zuerst den Raktorkern im Zentrum des Schiffes, und dann die sich langsam aufbauenden Ebenden.....und man fragt sich dabei "warum ersticken die nicht"?

[McWire]

Ja, mir sind diese Modelle bekannt:
Wiki.
Mir leuchtet auch deine Logik ein.

In der Geometrie hast du damit sicher recht:
Natürlich sind es Kreise die eine Kugel in einer Flächenwelt formt (beginnend und endend mit einem Punkt). Was der Flächenweltbewohner wahrnimmt sind die Umfänge der Kreise - welche der Schatten der Kugel sind. Richtig?

Aber WARUM sollte der Betrachter aus der 3D-Welt NUR die Oberflächen der 3D-Kugel sehen - welche der Schatten der 4D-Kugel sind - die sich langsam zur maximalen Größe ausdehnen, OHNE die sich (möglicher Weise) verändernde Position des Kugel-Mittelpunktes im Raum?
Und WENN sich dieser Mittelpunkt - da er aus dem Hyperraum kommt - Z.B. in einer 1/1000 Sekunde von einem weit entfernten Ort (im 3D-Raum), plötzlich in Sichtweite des Betrachter bewegt, DANN sieht der Betrachter doch zwangsläufig - Peng - eine Kugel die "einen Augenblick zuvor" noch nicht da war.

Außerdem trifft das mit den sich ausdehnenden Oberflächen, doch NUR auf eine reine geometrische Kugel (im wahrsten Sinne des Wortes) zu.
Oder sieht man z.B. beim Todesstern zuerst den Raktorkern im Zentrum des Schiffes, und dann die sich langsam aufbauenden Ebenden.....und man fragt sich dabei "warum ersticken die nicht"?

Ich denke, man sollte diese Hyperkugel/Hyperraum-Diskussion langsam mal vom Thread abtrennen und in einen eigenen Thread verschieben... hätte nicht gedacht, dass es eine so lange Off-Topic-Diskussion wird.

Im 3D-Raum kann man immer nur eine einzige "Ebene" eines 4D-Objektes sehen, da wir nunmal nur 3 der 4 Raumrichtungen wahrnehmen können.

Ob wir die Schnittebene des Objekt vollständig sehen können oder ob wir nur die Oberfläche sehen, hängt davon ab wie transparent das Material im 3D-Raum erscheint. Jedoch werden wir niemals gleichzeitig Rand und Mittelpunkt der Hyperkugel sehen können, da diese einen Abstand entlang der Hyperachse besitzen.... genausowenig wird ein hypothetischer 2D-Beobachter jemals zwei Punkte einer 3D-Kugel sehen können, welche eine unterschiedliche Höhe/Tiefe haben, da er diese Dimension nicht wahrnehmen kann.

Der Todesstern selbst ist ja nur 3-dimensional und somit aus "Sicht" des Hyperraum flach, er würde, da er nur aus einer Schnittebene besteht, sofort vollständig sichtbar. Dies gilt allerdings nur, wenn er im richtigen (senkrechten) Winkel in den Normalraum zurückkommt, ansonsten würden sich nur einzelne Schichten im Normalraum materialisieren.

[arthur]

Ich sagte ja bereits (oder vielmerhr, ich nahm es an), daß wir das 4D-3D-Problem nicht gänzlich mit dem 3D-2D-Problem vergleichen können. Jedenfalls nicht solange wir uns NUR an der Geometrie orientieren. Die Frage nach dem "visuellen Effekt" können wir nur klären, wenn wir die Reltivitätsdtheorie mit einbeziehen.
Und die greift nun mal mindestens dann, wenn die Zeit eine Rolle spielt.

Die Zeit ist relativ. 2 Betrachter nehmen Geschwindigkeit auf unterschiedliche Weise wahr, so die Theorie.

Ich stelle mir das so vor:
Der Hyperraumbewohner verharrt auf seinem "Bahnsteig" und sieht wie sich der RAUM bewegt. Z.B. die Krümmung des Raumes........
Der Betrachter im 3D-Raum sieht ein Raumschiff, daß auf Lichtgeschwindigkeit beschleunigt und dann vor seinen Auge "verschwindet". Peng, weg.
Der Betrachter im Hyperraum sah das selbe Raumschiff aber stehts auf der selben Position verharren. Aus seiner Sicht hat sich das Raumschiff NIE bewegt. Für ihn spielt Zeit und Raum keine Rolle. Denn das sind letztenendes auch nur geometrische Größen, die wir herranziehen um uns das Phänomen erklären zu können.
Der Hyperraumbewohner weiss, dass sich das Raumschiff im 3D-Raum bewegte und sich nun vollständig in seiner Welt befindet. Er würde auch wissen wann es im 3D-Raum wieder unter Lichtgschwindigkeit fällt und somit wieder für die 3D-Bewohner sichtbar wird.
Aber Bewegung und Zeit spielt dabei für ihn keine Rolle.

Für uns gelten keine Hyperraumgesetze. Daher wissen wir auch nicht ob die Hyperkugel wirklich eine Kugel ist. Wir SEHEN eine Kugel. Wir sehen aber nicht wie die Hyperraum"kugel" aussieht. Wir können das nur für unsere Welt (geometrisch) eingrenzen. Der Flächenbewohner grenzt auch die Kugel ein.....in einen "dreidmensionalen Kreis". Eine andere Möglichkeit hat er nicht. Für UNS ist das Ding einfach eine Kugel. Aber um dem Flächenbewohner seine Welt erklären zu können, reduzieren wir die Kugel auf für ihn verständliche Kreise. Nicht mehr und nicht weniger.
Der Flächenbewohner sieht aber niemals die vollständigen Flächen dieser Kreise (denn dazu müsste er sich in den 3D-Raum begeben), allenfalls die vollständigen Umfänge. Und wir sehen niemals eine vollständige Kugel (denn dazu müssten wir uns in den Hyperraum begeben), allenfalls die vollständige Oberfläche.
Die vollständige Kugel sieht NUR der Hyperraumbewohner, da er in der Lage ist sie als Hyperraumkugel zu sehen, so wie wir in der Lage sind eine 3D-Fläche zu sehen.

Der Todesstern selbst ist ja nur 3-dimensional und somit aus "Sicht" des Hyperraum flach, er würde, da er nur aus einer Schnittebene besteht, sofort vollständig sichtbar.

Soweit kann ich folgen.

Dies gilt allerdings nur, wenn er im richtigen (senkrechten) Winkel in den Normalraum zurückkommt, ansonsten würden sich nur einzelne Schichten im Normalraum materialisieren.

Schichten sind Flächen. Im Hyperraum ist die "Fläche" allerdings dreisimensional.
Also müssten sich in unserer "flachen" Welt zumindest räumliche "Schichten" materialisieren - also Objekte bzw. Teile von Objekten.
Es ist egal wie wir das nennen, wir können nicht weniger als 3D-Objekte visuell wahrnehmen. Auch wenn wir nur mit einem Auge schauen.

[McWire]

Ich sagte ja bereits (oder vielmerhr, ich nahm es an), daß wir das 4D-3D-Problem nicht gänzlich mit dem 3D-2D-Problem vergleichen können. Jedenfalls nicht solange wir uns NUR an der Geometrie orientieren. Die Frage nach dem "visuellen Effekt" können wir nur klären, wenn wir die Reltivitätsdtheorie mit einbeziehen.
Und die greift nun mal mindestens dann, wenn die Zeit eine Rolle spielt.

Das ganze ist ein rein geometrisches Problem und darin hat die Zeit erstmal nix zu suchen.
Ich habe nur die Frage beantwortet, wie eine 4D-Hyperkugel in einer 3D-"Ebene" innerhalb des Hyperraums erscheinen würde und zwar auch unter der Vorraussetzung, dass es eine Zeit gibt und diese Hyperkugel sich durch die 3D-"Ebene" bewegen würde.
Ich habe nur diese 3D-"Ebene" mit dem RZ-Kontinuum gleichgesetzt, da es ja ein 3D-Raum ist, wobei es zusätzlich noch eine nichträumlich-nichtgeometrische Dimension in Form der Zeit gibt.
Und ich habe nebenbei noch angenommen, dass die Zeit auch im Hyperraum gilt, da sich sonst die Hyperkugel nicht durch das RZ-Kontinuum bewegen könnte... aber das nur so am Rande.

Die korrekte visuelle Reihenfolge der Schnittbilder wäre jedenfalls:

Punkt (Pol)
Kugeln mit ansteigendem Radius
Kugel mit äquatorialer, also maximaler Ausdehnung (Äquatoreben steht senkrecht auf der Verbindungslinie von Pol und Gegenpol)
Kugeln mit abnehmenden Radius
Punkt (Gegenpol)

Alles andere erfordert, dass entweder der Normalraum oder der Hyperraum gekrümmt wäre oder das die Geometrie auf das RZ-Kontinuum und den Hyperraum nicht angewendet werden kann.
Zumindestens für das RZ-Kontinuum ist aber eine euklidische Geometrie bestätigt, also eine unendlich geringe Krümmung... alle bisherigen Analysen sprechen von einem sehr flachen Raumkontinuum.

Nochmal:

Eine Kugel ist eine um eine Raumdimension verkürzte Hyperkugel und ein Kreis ist ein um eine Dimension verkürzte Kugel.

[Agent Scullie]

Kommt drauf an in welcher Form sie vorliegt. Normale Materie kann bis auf 10^12 kg/cm³ komprimiert werden, was 10^18 kg/m³ entspricht.
Diese besondere Materiform kommt in Neutronensternen vor und kann nicht weiter komprimiert werden, da sonst ein schwarzes Loch entsteht.

Es gibt quantenmechanische Grenzen die nicht nur für reale Materie sondern auf für exotische Materie gilt. Bei einer Dichte um die 10^20 kg/m³ ist einfach Schluss, mehr Kompression würde eine Quantensingularität und damit ein SL erzeugen.

dass ein Neutronenstern bei Überschreiten der besagten Dichte zum schwarzen Loch kollabiert, hat nichts damit zu tun, dass es sich dabei um eine aus der QM folgende Grenzdichte handeln würde, sondern damit, dass wenn er diese Dichte erreichen soll, seine Masse nahe der Grenzmasse für Neutronensterne liegen muss. Ist seine Masse kleiner, so ist seine Eigengravitation nicht stark genug, ihn auf diese Dichte zu komprimieren, seine Dichte bleibt dann niedriger. Ist seine Masse höher, reicht der Entartungsdruck der Neutronen nicht mehr aus, um den Stern gegen die Gravitation abzustützen, und er kollabiert zu einem SL.

Die besagte Grenzdichte gilt also nur für den speziellen Fall, dass ein Gleichgewicht von Eigengravitation und Neutronen-Entartungsdruck vorliegt und keine nichtgravitativen Kräfte beteiligt sind. Bei einer Kompression, die durch nichtgravitative Kräfte bewirkt wird (oder auch durch gravitative Kräfte, die nicht von der Eigengravitation der zu komprimierenden Materiemenge herrühren), gibt es keine solche Grenzdichte. Die QM erlaubt es, Materie beliebig stark zu komprimieren, es tritt dann nur ein entsprechend starker Entartungsdruck auf, den man überkompensieren muss. Zur Bildung eines SL kommt es erst dann, wenn der Radius des von der komprimierten Materiemenge eingenommenen Volumens kleiner wird als der Schwarschild-Radius der Masse der Materiemenge. Die Dichte eines materiellen Objekts mit einer Masse von 10^12 kg z.B. würde bei Erreichen des Schwarschild-Radius bei 10^56 kg/m^3 liegen, also 10^36 mal höher als deine Grenzdichte-Angabe von 10^20 kg/m^3.

Nur in der Quantengrivation sieht es etwas anders aus, da kann man davon ausgehen, dass die Planck-Dichte von 10^97 kg/m^3 eine Obergrenze für die Dichte darstellt.

Auch den Begriff "Quantensingularität" gibt es in der heutigen Physik nicht. Die Singularität im Zentrum eines SL heißt einfach Singularität, insbesondere ergibt sie sich aus einer klassischen Theorie (der ART), nicht aus einer Quantentheorie.


.
EDIT (autom. Beitragszusammenführung) :
Agent Scullie schrieb nach 13 Minuten:

Das RZ-Kontinuum hat sowie einen Grenzwert, nämlich die Planck-Werte.
Die Planckzeit beträgt 10^-43 s, daraus ergibt sich durch c die Plancklänge zu 9*10^-27 m,

eher 10^-35 m:

Planck-Einheiten ? Wikipedia

Ein Elektron hat beispielsweise 3*10^-15 m Radius,

das ist der Radus, der sich ergibt, wenn man annimmt, die Masse des Elektron bestehe vollständig aus der potentiellen Energie der elektrischen Ladung des Elektrons im eigenen elektrischen Feld (der sog. Selbstenergie). Es ist aber ein experimentelles Faktum, dass dieser Radius nichts mit dem tatsächlichen Radius zu tun hat. Aus Streuexperimenten weiß man, dass der Elektronenradius unterhalb von 10^-22 m liegen muss, also viel kleiner. Die "nackte" Masse des Elektrons, die es hätte wenn seine elektrische Ladung nicht da wäre, muss demnach negativ sein.
In der gewöhnlichen Quantenfeldtheorie, ohne Berücksichtigung der Gravitation, nimmt man allgemein an, dass elementare Teilchen wie Leptonen und Quarks punktförmig sind, ihr Radius somit null ist. In der Stringtheorie wären sie Strings, mit einer Länge gleich der Planck-Länge. Für die Dichte erhält man in beiden Fällen unendlich.

[McWire]

dass ein Neutronenstern bei Überschreiten der besagten Dichte zum schwarzen Loch kollabiert, hat nichts damit zu tun, dass es sich dabei um eine aus der QM folgende Grenzdichte handeln würde, sondern damit, dass wenn er diese Dichte erreichen soll, seine Masse nahe der Grenzmasse für Neutronensterne liegen muss. Ist seine Masse kleiner, so ist seine Eigengravitation nicht stark genug, ihn auf diese Dichte zu komprimieren, seine Dichte bleibt dann niedriger. Ist seine Masse höher, reicht der Entartungsdruck der Neutronen nicht mehr aus, um den Stern gegen die Gravitation abzustützen, und er kollabiert zu einem SL.

Die besagte Grenzdichte gilt also nur für den speziellen Fall, dass ein Gleichgewicht von Eigengravitation und Neutronen-Entartungsdruck vorliegt und keine nichtgravitativen Kräfte beteiligt sind. Bei einer Kompression, die durch nichtgravitative Kräfte bewirkt wird (oder auch durch gravitative Kräfte, die nicht von der Eigengravitation der zu komprimierenden Materiemenge herrühren), gibt es keine solche Grenzdichte. Die QM erlaubt es, Materie beliebig stark zu komprimieren, es tritt dann nur ein entsprechend starker Entartungsdruck auf, den man überkompensieren muss. Zur Bildung eines SL kommt es erst dann, wenn der Radius des von der komprimierten Materiemenge eingenommenen Volumens kleiner wird als der Schwarschild-Radius der Masse der Materiemenge. Die Dichte eines materiellen Objekts mit einer Masse von 10^12 kg z.B. würde bei Erreichen des Schwarschild-Radius bei 10^56 kg/m^3 liegen, also 10^36 mal höher als deine Grenzdichte-Angabe von 10^20 kg/m^3.

Nur in der Quantengrivation sieht es etwas anders aus, da kann man davon ausgehen, dass die Planck-Dichte von 10^97 kg/m^3 eine Obergrenze für die Dichte darstellt.

Auch den Begriff "Quantensingularität" gibt es in der heutigen Physik nicht. Die Singularität im Zentrum eines SL heißt einfach Singularität, insbesondere ergibt sie sich aus einer klassischen Theorie (der ART), nicht aus einer Quantentheorie.


.
EDIT (autom. Beitragszusammenführung) :
Agent Scullie schrieb nach 13 Minuten:

eher 10^-35 m:

Planck-Einheiten ? Wikipedia

das ist der Radus, der sich ergibt, wenn man annimmt, die Masse des Elektron bestehe vollständig aus der potentiellen Energie der elektrischen Ladung des Elektrons im eigenen elektrischen Feld (der sog. Selbstenergie). Es ist aber ein experimentelles Faktum, dass dieser Radius nichts mit dem tatsächlichen Radius zu tun hat. Aus Streuexperimenten weiß man, dass der Elektronenradius unterhalb von 10^-22 m liegen muss, also viel kleiner. Die "nackte" Masse des Elektrons, die es hätte wenn seine elektrische Ladung nicht da wäre, muss demnach negativ sein.
In der gewöhnlichen Quantenfeldtheorie, ohne Berücksichtigung der Gravitation, nimmt man allgemein an, dass elementare Teilchen wie Leptonen und Quarks punktförmig sind, ihr Radius somit null ist. In der Stringtheorie wären sie Strings, mit einer Länge gleich der Planck-Länge. Für die Dichte erhält man in beiden Fällen unendlich.

1.) Das Wort "Quantensingularität" ist ein pure Gewohnheit eines Star Trek Fan.

2.) Ich ging nur von der Eigenschwerkraft, der elektromagnetischen Abstoßung und den beiden Kernkräften der Materie aus, als ich die Dichte angegeben habe. Defakto kann man auf natürlichem Wege die Materie nicht stärker komprimieren, es würde immer ein schwarzes Loch entstehen. Es gäbe natürlich trotzdem die Möglichkeit von exotischen Partikeln höherer Dichte, die aber mit normaler Materie nix mehr zu tun haben.

3.) Heißt das jetzt, dass ich, um die Planck-Länge in Planck-Zeit zurückzulegen Überlichtgeschwindigkeit erreichen muss? -> Vergesst diese Frage... ich habe wohl einen Rechenfehler gemacht, die 10^35 m sind korrekt... ich habe aus Versehen mit c² gerechnet

4.) Die Werte für das Elektron habe ich einem physikalischen Taschenbuch entnommen. Den Autor sollte man vielleicht auf den Fehler hinweisen^^


.
EDIT (autom. Beitragszusammenführung) :
McWire schrieb nach 17 Minuten und 9 Sekunden:

Korrigierter Absatz:

Das RZ-Kontinuum hat sowie einen Grenzwert, nämlich die Planck-Werte.
Die Planckzeit beträgt 5,4*10^-44 s, daraus ergibt sich durch c die Plancklänge zu 1,62*10^-25 m, das Planck-Volumen (für eine Kugel): 1,78*10^-104 m³.... ein kleineres Kugel-Volumen kann es nicht geben. Dementsprechend muss Materie, da es eine endliche Ausdehnung besitzt, eine endliche Anzahl von Masse pro Raumvolumen haben.

Daraus ergibt sich sich aufgrund der Planck-Masse zu 2,18*10^-8 kg eine theoretische Maximaldichte von 1,22*10^96 kg/m³ für ein Kugelvolumen... weniger als die 5,16*10^96 der Planck-Dichte.


.
EDIT (autom. Beitragszusammenführung) :
McWire schrieb nach 16 Minuten und 10 Sekunden:

Korrigierter Absatz:

Schwierig sind Treibstoff und Vorräte, die das letzte Drittel ausmachen.
Vorräte dürften so bei 100 kg/m³ liegen, was Flüssigkeiten entspricht.
Treibstoff in Form von gewöhnlichem Wasserstoff oder Deuterium zum einem hat eine Dichte von 0,17 kg/m³. Die Dichte der Hypermaterie kann ich nicht genau einschätzen dürfte aber deutlich über den anderen Dichten liegen... nehmen wir dafür einfach mal 5,2*10^96 kg/m³ an, dem maximal möglichen was für gewöhnliche Materie geht.

Wenn der Treibstoff 50% von den Vorräten ausmacht:

m(Treibstoff)=5,2*10^96 kg/m³ * 1/3 * 3,8*10^17 m³
m(Treibstoff)=6,6*10^113 kg

Somit macht der Treibstoff die Hauptmasse des Todessterns aus, obwohl er nur 1/6 des Volumen ausmacht.
Den Rest braucht man schon garnicht mehr zu berechnen, da es nicht ins Gewicht fällt.

Damit hätte der Todestern 3*10^83 Sonnenmassen, was mehr Masse wäre als die gesamte sichtbare und dunkle Materie im Universum zusammen.

Geht man mal davon aus, dass die Crew den Dienst an Bord mehr als eine Planck-Zeit überleben soll, dann gibt es eine weitere Obergrenze für die Masse, die sich aus der Fallbeschleunigung ergibt.

a(Fall)=m/r²*G

a(Fall) soll höchsten 20 m/s² betragen, also ~2g, da der Radius des TS I 8*10^4 m beträgt, ergibt sich die maximale Masse zu 2*10^21 kg.

Damit kann die Hypermaterie eine maximale Dichte von 15110 kg/m³ haben, was etwa der 1,3-fachen Dichte von Blei entspricht.


.
EDIT (autom. Beitragszusammenführung) :
McWire schrieb nach 6 Minuten und 17 Sekunden:

Übrigends, um mal den SW-Techno-Fanatikern ein wenig Wind aus den Segeln zu nehmen, laut Planck-Einheiten ? Wikipedia ist bei ca 10^52 Watt Schluss, mehr Leistung kann kein Reaktor der Welt erzeugen, welcher den heute bekannten physikalischen Gesetzen unterliegt... ist zwar immernoch das 10^26-fache der Sonne, aber trotzdem eine absolute Grenze für jede Superwaffe. Der Superlaser kommt mit ca 10^38 W schon erheblich näher als ein Stern.

[Agent Scullie]

2.) Ich ging nur von der Eigenschwerkraft, der elektromagnetischen Abstoßung und den beiden Kernkräften der Materie aus, als ich die Dichte angegeben habe. Defakto kann man auf natürlichem Wege die Materie nicht stärker komprimieren, es würde immer ein schwarzes Loch entstehen.

dann solltest du aber berücksichtigen, dass es dann nicht nur eine Grenzdichte, sondern auch eine Grenzmasse gibt. Überschreitet ein Neutronenstern diese Grenzmasse (die bei 2-3 Sonnenmassen liegt), so kollabiert er zum schwarzen Loch. Deine Rechnung, nach der der Todesstern 10^83 Sonnenmassen haben soll, kann daher nicht richtig sein.

4.) Die Werte für das Elektron habe ich einem physikalischen Taschenbuch entnommen. Den Autor sollte man vielleicht auf den Fehler hinweisen^^

dieser Fehler ist leider sehr verbreitet, den auf diese Weise berechneten Elektronenradius als "klassischen Elektronenradius" auszuweisen, ohne weitere Erläuterung.

Korrigierter Absatz:

Schwierig sind Treibstoff und Vorräte, die das letzte Drittel ausmachen.
Vorräte dürften so bei 100 kg/m³ liegen, was Flüssigkeiten entspricht.
Treibstoff in Form von gewöhnlichem Wasserstoff oder Deuterium zum einem hat eine Dichte von 0,17 kg/m³. Die Dichte der Hypermaterie kann ich nicht genau einschätzen dürfte aber deutlich über den anderen Dichten liegen... nehmen wir dafür einfach mal 5,2*10^96 kg/m³ an, dem maximal möglichen was für gewöhnliche Materie geht.

Wenn der Treibstoff 50% von den Vorräten ausmacht:

m(Treibstoff)=5,2*10^96 kg/m³ * 1/3 * 3,8*10^17 m³
m(Treibstoff)=6,6*10^113 kg

Somit macht der Treibstoff die Hauptmasse des Todessterns aus, obwohl er nur 1/6 des Volumen ausmacht.
Den Rest braucht man schon garnicht mehr zu berechnen, da es nicht ins Gewicht fällt.

Damit hätte der Todestern 3*10^83 Sonnenmassen,

ehrlich gesagt ist mir noch nicht klar geworden, warum du die ganze Zeit mit so irrsinnig hohen Werten für die Dichte dieser Hypermaterie (oder des Treibstoffes) rechnest??
Schon Neutronensterndichte würde ich für viel zu hoch angesetzt halten.

Geht man mal davon aus, dass die Crew den Dienst an Bord mehr als eine Planck-Zeit überleben soll, dann gibt es eine weitere Obergrenze für die Masse, die sich aus der Fallbeschleunigung ergibt.

a(Fall)=m/r²*G

a(Fall) soll höchsten 20 m/s² betragen, also ~2g, da der Radius des TS I 8*10^4 m beträgt, ergibt sich die maximale Masse zu 2*10^21 kg.

Damit kann die Hypermaterie eine maximale Dichte von 15110 kg/m³ haben, was etwa der 1,3-fachen Dichte von Blei entspricht.

irgendetwas stimmt an deiner Rechnung nicht: die mittlere Dichte der Erde liegt ja schon bei 5000 kg/m^3, und bei einem Erdradius von 6000 km ergibt sich gerade mal eine Fallbeschleunigung von 1 g. Die Fallbeschleunigung eines Himmelskörpers vorgegebener Dichte sollte aber linear mit dem Radius ansteigen. Die Fallbeschleunigung auf der Oberfläche eines Körpers mit der gleichen Dichte wie der Erde, aber einem Radius von von nur 80 km, sollte daher bei 80/6000 g = 0.013 g liegen. Die dreifache Dichte von 15000 kg/m^3 sollte das ganze auch nur um den Faktor drei vergrößern, also 0.04 g.

Übrigends, um mal den SW-Techno-Fanatikern ein wenig Wind aus den Segeln zu nehmen, laut Planck-Einheiten ? Wikipedia ist bei ca 10^52 Watt Schluss, mehr Leistung kann kein Reaktor der Welt erzeugen, welcher den heute bekannten physikalischen Gesetzen unterliegt...

wie kommst du denn darauf? Es sind ja nicht alle Planck-Größen Grenzgrößen. Es gibt z.B. auch größere Massen als die Planck-Masse. Daher sollte es auch kein Problem sein, höhere Leistungen als die Planck-Leistung zu erzeugen. Nur höhere Leistungsdichten als die Planck-Leistungsdichte (Planck-Leistung durch Planck-Fläche) wären schwierig.

[arthur]

Das ganze ist ein rein geometrisches Problem und darin hat die Zeit erstmal nix zu suchen.
Ich habe nur die Frage beantwortet, wie eine 4D-Hyperkugel in einer 3D-"Ebene" innerhalb des Hyperraums erscheinen würde und zwar auch unter der Vorraussetzung, dass es eine Zeit gibt und diese Hyperkugel sich durch die 3D-"Ebene" bewegen würde.

Dann reden wir die ganze Zeit aneinander vorbei. Ich habe nämlich sehr wohl die Zeit mit einbezogen. Wobei ich es mir mit einem eindeutigen geometrischen Modell schwer tue, wenn ich den visuellen Effekt "erraten" will. Und das ist ja die Frage die wir am Anfang unserer Diskussion gestellt haben. Die Frage nach dem visuellen Effekt.

Und ich habe nebenbei noch angenommen, dass die Zeit auch im Hyperraum gilt, da sich sonst die Hyperkugel nicht durch das RZ-Kontinuum bewegen könnte...

Ja die Zeit gilt im Hyperraum, aber nur für die Kugel und nicht für den Betrachter im Hyperraum.
Der Betrachter im 3D-Raum faltet das Blatt Papier von links nach rechts zusammen. Der Punkt auf dem Blatt Papiert berührt nun die linke und rechte Seite des Blattes gleichzeitig. Für den Betrachter im 3D-Raum hat sich aber der Punkt selbst keinen Millimeter bewegt. Selbst wenn dieser das Blatt Papier andersrum (also die jetzt unten liegende Seite von rechts nach links) aufklappt, so daß der Punkt aus seiner Sicht auf den Boden "schaut" (der Punkt hat natürlich keine Ahnung was ein Boden ist).
Nun kann der Punkt auf dem Blatt Papiert über die ganze Fläche geflitzt sein. Aber für den Betrachter im 3D-Raum hat sich der Punkt eben nicht von der Stelle bewegt. Er weiß aber daß der Punkt in seiner Flächenwelt eine enorme Strecke zurückgelegt hat, die er nun auf dem Blatt Papier einzeichnen könnte - und er muss sich dazu nicht von der Stelle bewegen.

Zusammenfassend heißt das doch:
In der 3D-Welt muss die Strecke des Punktes nicht zurückgelegt werden, damit dieser seinen Bestimmungsort in der Flächenwelt erreicht.
In der 3D-Welt hat sich auch außer dem Blatt Papier sonst nichts gekrümmt.
Im Hyperraum muss nicht die Zeit des Raumschiffes abgelaufen sein, damit dieses seinen Bestimmungsort im Raum erreicht.
Im Hypperraum hat sich ausser dem Raum nichts gekrümmt.

Punkt (Pol)
Kugeln mit ansteigendem Radius
Kugel mit äquatorialer, also maximaler Ausdehnung (Äquatoreben steht senkrecht auf der Verbindungslinie von Pol und Gegenpol)
Kugeln mit abnehmenden Radius
Punkt (Gegenpol)

Ich bezweifle nicht daß das in der Geometrie so aussieht.
In "meiner" Geometrie sieht das mit der Kugel eher so aus:

(im Hyperraum krümmt sich der Raum, Wurmlöcher werden gebildet und der Raum bewegt sich schlißlich so, daß das Raumschiff seinen Bestimmungsort "auf" dem Raumgitter erreicht.)

(in der 3D-Welt bewegt sich das Raumschiff "auf" dem Raumgitter mit abartiger Geschwindigkeit - so schnell daß es nicht mehr gesehen wird. Es befindet sich im Hyperraum)

Zumindestens für das RZ-Kontinuum ist aber eine euklidische Geometrie bestätigt, also eine unendlich geringe Krümmung... alle bisherigen Analysen sprechen von einem sehr flachen Raumkontinuum.

Der Begriff hat jedoch sehr verschiedene Aspekte und lässt Verallgemeinerungen zu. (Wiki)

Eine Kugel ist eine um eine Raumdimension verkürzte Hyperkugel und ein Kreis ist ein um eine Dimension verkürzte Kugel.

Wir haben es aber immer noch mit einem Raumschiff zu tun und nicht mit einer "Kugel" auf dem Reissbrett. Der Todesstern muß erst die Schwelle zur Lichtgeschwindigkeit überwinden.
Für die Besatzung des Todessterns beschleunigt sich die Zeit außerhalb des Schiffes und aus unserer Sicht vergeht an Bord das Todessterns die Zeit immer langsamer. Der Todesstern wird aus unserer Sicht immer kürzer und flacher bis er nicht mehr zu sehen ist.
Es finden eben seltsame Veränderungen statt.
Wenn er aus dem Hyperraum zurückkommt müsste etwas ähnlich zu beobachten sein.

[McWire]

dann solltest du aber berücksichtigen, dass es dann nicht nur eine Grenzdichte, sondern auch eine Grenzmasse gibt. Überschreitet ein Neutronenstern diese Grenzmasse (die bei 2-3 Sonnenmassen liegt), so kollabiert er zum schwarzen Loch. Deine Rechnung, nach der der Todesstern 10^83 Sonnenmassen haben soll, kann daher nicht richtig sein.

Es ist eine hypothetisch-mathematische Angabe. Wenn man in das Volumen eines Todesstern 10^83 Sonnenmassen packt, so kommt man auf die Planck-Dichte. Meine Rechnung geht natürlich davon aus, dass sich die Dichte der Materie nicht ändert, sie also nicht durch die Eigenschwerkraft komprimiert wird. Erachte es einfach als Rechenspielchen.

dieser Fehler ist leider sehr verbreitet, den auf diese Weise berechneten Elektronenradius als "klassischen Elektronenradius" auszuweisen, ohne weitere Erläuterung.

Bei Wikipedia ist exakt diese Zahl auch angegeben. Aber Danke für die Korrektur, da wäre ich wohl nicht so schnell drauf gekommen, ausser vielleicht wenn ich in paar Jahren endlich mal dieses Buch über Elementarteilchenphysik durch habe, was ich mir vor 3 Jahren mal gekauft habe.

ehrlich gesagt ist mir noch nicht klar geworden, warum du die ganze Zeit mit so irrsinnig hohen Werten für die Dichte dieser Hypermaterie (oder des Treibstoffes) rechnest??
Schon Neutronensterndichte würde ich für viel zu hoch angesetzt halten.

Dies ist ein Star Wars-Forum, da werden keine halben Sachen gemacht.
Werte unter 10^30 gelten geradezu als unschick.

Spaß beiseite... es ging darum zu erklären, wie der Todessternreaktor mehrere Wochen oder Jahre lang eine Leistung von 10^38 Watt (die notwendig sind um einen erdähnlichen Planeten in weniger als 10 Sekunden vollständig zu zerstören) für den Superlaser bereitsstellen kann. Die Frage ist also, welche Dichte die Hypermaterie haben muss, damit man über E=mc² dauerhaft eine so hohe Leistung bereitstellen kann. Ich für meinen Teil halte diese ganzen irrsinnigen Energie-Angaben für absoluten Unsinn, da alleine aufgrund der Energieerhaltung im Universum solch ein Energiebedarf mit normalen Mitteln niemals solange gedeckt werden kann. Ich tue nur den SW-Fans den Gefallen theoretische Rechnung aufzustellen, die zumindestens hypothetisch diese Möglichkeit offen lassen.

Um 10^38 Watt 1 Jahr lang bereitstellen zu können, braucht man ca 10^45 Joule. Nach E=mc² ergibt das ein Masseäquivalent von ca 10^29 kg.

Will man also in dem Todessternvolumen von ca 10^17 m³ mindestens 10^29 kg Materie unterbekommen, muss diese eine Mindestdichte von 10^12 kg/m³ haben. Allerdings hätte des TS dann eine Schwerkraft, die jeden Menschen im Inneren augenblicklich zerquetschen würde.

irgendetwas stimmt an deiner Rechnung nicht: die mittlere Dichte der Erde liegt ja schon bei 5000 kg/m^3, und bei einem Erdradius von 6000 km ergibt sich gerade mal eine Fallbeschleunigung von 1 g. Die Fallbeschleunigung eines Himmelskörpers vorgegebener Dichte sollte aber linear mit dem Radius ansteigen. Die Fallbeschleunigung auf der Oberfläche eines Körpers mit der gleichen Dichte wie der Erde, aber einem Radius von von nur 80 km, sollte daher bei 80/6000 g = 0.013 g liegen. Die dreifache Dichte von 15000 kg/m^3 sollte das ganze auch nur um den Faktor drei vergrößern, also 0.04 g.

Kann sein, dass ich mich in der Hektik verrechnet habe... zumal ich zu dem Zeitpunkt noch unter Alkohol stand^^

Todesstern I ist eine Kugel mit einem Durchmesser von 160 km, damit ein Radius von 80.000 m.
Nach V=4/3*pi*r³ ergibt sich ein Kugelvolumen zu 2,1*10^15 m³.

Todesstern II ist eine Kugel mit einem Durchmesser von 900 km, damit ein Radius von 450.000 m.
Nach ... ergibt sich ein Kugelvolumen zu 3,8*10^17 m³

Bei beiden soll 1/3 des Volumens aus Treibstoff sprich Hypermaterie bestehen... wobei das relativ hoch gegriffen ist.

Die Fallbeschleunigung an der Oberfläche soll auf beiden Station 2g, also 20 m/s², nicht übersteigen.

Für TS I ergibt sich aus der Formel für die Fallbeschleunigung eine Maximal-Gesamtmasse zu 1,9*10^21 kg, für TS II eine maximale Gesamtmasse zu 6,1*10^22 kg.

Damit ergibt sich für die Hypermaterie eine maximale Dichte zu 2,71 Mio kg/m³ für TS I bzw 482.000 kg/m³ für TS II, wenn diese jeweils 1/3 des Stationsvolumen ausmachen würde.

wie kommst du denn darauf? Es sind ja nicht alle Planck-Größen Grenzgrößen. Es gibt z.B. auch größere Massen als die Planck-Masse. Daher sollte es auch kein Problem sein, höhere Leistungen als die Planck-Leistung zu erzeugen. Nur höhere Leistungsdichten als die Planck-Leistungsdichte (Planck-Leistung durch Planck-Fläche) wären schwierig.

Ich habe dich und die Wikipedia nunmal so verstanden, dass die Planck-Größen die Grenze dessen angeben, was sich mit unseren physikalischen Mitteln noch beschreiben lässt.
Selbst wenn man alle Materie und Energie im Universum zusammen nimmt, erreicht man die Planck-Leistung und Planck-Masse nicht.
Solange die Energieerhaltung gilt, ist dies sowieso eine rein hypothetische Diskussion, da alleine das natürliche Vorkommen von Materie und Energie im Universum uns eine absolute Grenze aufzwingt.


.
EDIT (autom. Beitragszusammenführung) :
McWire schrieb nach 3 Minuten und 9 Sekunden:

Dann reden wir die ganze Zeit aneinander vorbei.

Richtig. Ich habe die Diskussion so verstanden, dass es um das hypothetische Problem des Durchfluges einer 4D-Hyperkugel durch unser RZ-Kontiunuum geht. In diesem Fall wäre meine geometrische Beschreibung vermutlich korrekt.

Wenn es aber darum geht, den Hyperraumsprung eines Todesstern zu erklären, so kann man sich die ganze Mühe sparen, da dieser eh nur dreidimensional ist und somit in einem Stück in den Normalraum zurück kommt. Die Sprungdauer soll laut irgendeiner populärwissenschaftlichen Publikation (Star-Observer-Beitrag zu Scifi-Hyperraumtechnologie von vor etwa 10 Jahren) der Planck-Zeit entsprechen.

[Agent Scullie]

Spaß beiseite... es ging darum zu erklären, wie der Todessternreaktor mehrere Wochen oder Jahre lang eine Leistung von 10^38 Watt (die notwendig sind um einen erdähnlichen Planeten in weniger als 10 Sekunden vollständig zu zerstören) für den Superlaser bereitsstellen kann.

also erstmal ist mir nicht ganz klar, wie ihr auf die 10^38 Watt kommt. Die Energie, die notwendig wäre, um die Erde in die Luft (oder besser: in den Weltraum) zu sprengen, sollte gleich der gravitativen Bindungsenergie sein, die bei 2,4 * 10^32 Joule liegt:

Bindungsenergie ? Wikipedia

Will man diese in 10 Sekunden aufbringen, bräuchte man somit 2,4 *10^31 Watt, also 10^7 mal weniger als 10^38 Watt.

Zum zweiten feuert der Todesstern ja nicht die ganze Zeit. Man kann davon ausgehen, dass das Feuern eine Lastspitze darstellt und der Reaktor sonst eine viel niedrigere Leistung fährt. Die zum Aufbringen der 2,4 * 10^32 J nötige Masse gemäß E=mc^2 liegt bei 2,6 * 10^15 kg. Nimmt man an, dass der Todesstern genug Brennstoff für mehrere Abschüsse mitführt, sagen wir 50, macht das 1,3 * 10^17 kg. In einem Todessternvolumen von V = 4pi/3 R^3 = 4pi/3 (8*10^5 m)^3 = 2*10^15 m^3 sollten die bequem Platz finden

Ich habe dich und die Wikipedia nunmal so verstanden, dass die Planck-Größen die Grenze dessen angeben, was sich mit unseren physikalischen Mitteln noch beschreiben lässt.

das trifft auf einige der Planck-Größen zu, aber nicht auf alle.

Selbst wenn man alle Materie und Energie im Universum zusammen nimmt, erreicht man die Planck-Leistung und Planck-Masse nicht.

die Planck-Masse ist offensichtlich kein Problem: die liegt bei 10^-8 kg, aus unserem Alltag kennen wir viele Objekte mit größerer Masse

[McWire]

also erstmal ist mir nicht ganz klar, wie ihr auf die 10^38 Watt kommt. Die Energie, die notwendig wäre, um die Erde in die Luft (oder besser: in den Weltraum) zu sprengen, sollte gleich der gravitativen Bindungsenergie sein, die bei 2,4 * 10^32 Joule liegt:

Bindungsenergie ? Wikipedia

Will man diese in 10 Sekunden aufbringen, bräuchte man somit 2,4 *10^31 Watt, also 10^7 mal weniger als 10^38 Watt.

Zum zweiten feuert der Todesstern ja nicht die ganze Zeit. Man kann davon ausgehen, dass das Feuern eine Lastspitze darstellt und der Reaktor sonst eine viel niedrigere Leistung fährt. Die zum Aufbringen der 2,4 * 10^32 J nötige Masse gemäß E=mc^2 liegt bei 2,6 * 10^15 kg. Nimmt man an, dass der Todesstern genug Brennstoff für mehrere Abschüsse mitführt, sagen wir 50, macht das 1,3 * 10^17 kg. In einem Todessternvolumen von V = 4pi/3 R^3 = 4pi/3 (8*10^5 m)^3 = 2*10^15 m^3 sollten die bequem Platz finden

das trifft auf einige der Planck-Größen zu, aber nicht auf alle.

die Planck-Masse ist offensichtlich kein Problem: die liegt bei 10^-8 kg, aus unserem Alltag kennen wir viele Objekte mit größerer Masse

Es ist ja nicht damit getan die Bindungsenergie des Planeten zu überwinden, sondern seine Masse wird ja zudem noch in Sekundenbruchteile auf eine relativ hohe Geschwindigkeit beschleunigt.
Im übrigen habe ich Verwechslungsfehler begangen, es sind 10^38 Joule nicht Watt. -> http://www.scifi-forum.de/science-fi...-wirklich.html

Daraus ergeben sich ~10^34 Watt, da die Aufladezeit ja einen Tag (86400 Sekunden) beträgt.
Bei 10^38 Joule brauche ich dann nur noch eine Dichte von 10^7 kg/m³, anstatt von 10^12 kg/m³ bei 10^45 Joule.

Sieh auch die Threads: http://www.scifi-forum.de/science-fi...ml#post1818590 und http://www.scifi-forum.de/science-fi...odesstern.html

Die Rechnung wurde schon reichlich oft durchgekaut, auch hier: Star Wars vs Star Trek Essays: Planet Killers und http://stardestroyer.net/Empire/Tech/Beam/Alderaan.html

[Agent Scullie]

Wir haben es aber immer noch mit einem Raumschiff zu tun und nicht mit einer "Kugel" auf dem Reissbrett. Der Todesstern muß erst die Schwelle zur Lichtgeschwindigkeit überwinden.
Für die Besatzung des Todessterns beschleunigt sich die Zeit außerhalb des Schiffes und aus unserer Sicht vergeht an Bord das Todessterns die Zeit immer langsamer. Der Todesstern wird aus unserer Sicht immer kürzer und flacher bis er nicht mehr zu sehen ist.
Es finden eben seltsame Veränderungen statt.

also was da zu lesen ist, kannst du aber vergessen. Zum einen würde man das Raumschiff durch das Teleskop nicht lorentz-kontrahiert sehen, da neben der Lorentz-Kontraktion noch ein weiterer Effekt zum Tragen kommt, der mit Lichtlaufzeiten zusammenhängt:

Der Ball ist rund

Hinzu kommt, dass die Insassen des Raumschiffes die Uhren auf der Erde nicht beschleunigt sehen, sondern ebenfalls verlangsamt. Das folgt aus dem Relativitätsprinzip, demzufolge beide, Erde und Raumschiff gleichberechtigt sind, da beide Inertialsysteme sind. Dass, wenn das Raumschiff irgendwann zur Erde zurückkehrt, beide feststellen, dass im Raumschiff weniger Zeit vergangen ist, hängt damit zusammen, dass das Raumschiff irgendwann eine Umkehrphase durchlaufen hat, in der es beschleunigt war und damit kein Inertialsystem mehr war, so dass die Gleichberechtigung nicht mehr gegeben ist:

Zwillingsparadoxon ? Wikipedia

Wenn er aus dem Hyperraum zurückkommt müsste etwas ähnlich zu beobachten sein.

darf ich fragen, wie du darauf kommst? Ich muss gestehen, ich habe nicht so wirklich verstanden, worüber ihr eigentlich am diskutieren seid, auch nach mehrmaligem Durchlesen eurer (deiner und McWire's) Postings nicht, aber soweit ich das mitbekommen habe, geht es ungefähr um folgendes: ihr stellt euch den Todesstern als 4-dim. Hyperkugel vor, diese existiert in einem 4-dim. Hyperraum, der sich aus den drei Dimensionen des Normalraumes und einer vierten Raumdimension zusammensetzt. Die Hyperkugel soll nun, während sie sich in Richtung der 4. Raumdimension bewegt, den 3-dim. Normalraum durchdringen, und ihr fragt euch, welchen visuellen Effekt das im 3D-Normalraum hat. Soweit richtig?

Will man da jetzt die Zeit berücksichtigen, so bildet diese mit den vier Raumdimensionen des Hyperraumes eine 5-dim. Raumzeit, mit der Zeit als fünfte, nicht-räumliche Dimension. Das kann man sich anschaulich so vorstellen, dass man zwei der drei Raumdimensionen des Normalraumes weglässt, dann bildet der Normalraum die x-Achse, der Hyperraum die x-y-Ebene, der hyperkugelförmige Todesstern einen Kreis in dieser Ebene, und die Zeit die z-Achse. Zu einem frühen Zeitpunkt, sagen wir z=0, befindet sich der Kreis vollständig bei y > 0, er schneidet die x-Achse nicht, und ein Beobachter auf der x-Achse (=Normalraum) bemerkt nichts von dem Kreis (im Normalraum ist nichts vom Todesstern zu sehen). Mit voranschreitender Zeit, also zunehmender z-Koordinate, wandert der Kreis auf die x-Achse zu, bei z=1 schneidet er die x-Achse in genau einem Punkt (Beobachter im Normalraum sieht einen Punkt vom TS), wandert dann (z>1) weiter in negative y-Richtung, so dass er seine Kreisfläche einen wachsenden endlichen Abschnitt der x-Achse schneidet (Beobachter sieht den TS als wachsende Kugel), bei z=2 liegt sein Mittelpunkt genau auf der x-Achse (Beobachter sieht TS in voller Größe), für z > 2 wandert der Kreis weiter in negative y-Richtung, sein Schnitt mit der x-Achse wird wieder kleiner (Beobachter sieht schrumpfenden TS), bei z=3 schneidet der Kreis die x-Achse wieder nur in einem Punkt, und bei z > 3 liegt der Kreis vollständig bei y < 0 (Beobachter sieht nichts mehr vom TS).

Relativistische Effekte wie Lorentz-Kontraktion können dabei eigentlich nur in Richtung der 4. Raumdimension auftreten, da sich der TS nur in dieser bewegt. Ein Beobachter im Normalraum sollte da also nichts von sehen. Allenfalls könnte es so sein, dass, weil der TS in Richtung der 4. Raumdimension lorentz-kontrahiert ist, der Zeitpunkt zu dem er den Normalraum zu schneiden beginnt, etwas später ist. Das aber auch nur, wenn die Geschwindigkeit des TS in Richtung der 4. Raumdimension nahe der Lichtgeschwindigkeit liegt, da nur dann relativistische Effekte auftreten.

Sprichst du hingegen von etwas völlig anderem, nämlich davon, dass der TS durch ein Wurmloch fliegt (deine Postings und Grafiken deuten so etwas an), sind ebenfalls keine relativistischen Effekte zu erwarten. Durch das Wurmloch hindurch fliegt der TS ja mit niedriger Unterlichtgeschwindigkeit. Ein Beobachter im Normalraum, der nichts vom Wurmloch weiß, und nur die TS-Positionen vor und nach der Wurmlochpassage registriert, hat zwar den Eindruck, der TS müsse mit vielfacher Lichtgeschwindigkeit geflogen sein, aber dessen Eindruck zählt für das Auftreten relativistischer Effekte nicht.

Die Zeit ist relativ. 2 Betrachter nehmen Geschwindigkeit auf unterschiedliche Weise wahr, so die Theorie.

Ich stelle mir das so vor:
Der Hyperraumbewohner verharrt auf seinem "Bahnsteig" und sieht wie sich der RAUM bewegt. Z.B. die Krümmung des Raumes........
Der Betrachter im 3D-Raum sieht ein Raumschiff, daß auf Lichtgeschwindigkeit beschleunigt und dann vor seinen Auge "verschwindet". Peng, weg.
Der Betrachter im Hyperraum sah das selbe Raumschiff aber stehts auf der selben Position verharren. Aus seiner Sicht hat sich das Raumschiff NIE bewegt.

hier scheinst du mir zwei Dinge durcheinanderzubringen, die nicht zusammengehören. Einerseits scheinst du von einem Raumantrieb zu sprechen, der auf einer Manipulation des Raumes beruht, anderseits führst du die Lorentzsche Geschwindigkeitsaddition an. Das passt nicht zusammen: die Lorentzsche Geschwindigkeitaddition gilt für zwei relativ zueinander bewegte Beobachter in einer flachen Raumzeit, wo weder Raum noch Raumzeit manipuliert werden. Wenn du aber schon einen Hyperraumbeobachter einführst, der noch dazu sehen soll, wie sich der Raum bewegt, und dann noch den Begriff Raumkrümmung verwendest, sieht es nicht so aus als ob diese Voraussetzungen erfüllt wären.

Und WENN sich dieser Mittelpunkt - da er aus dem Hyperraum kommt - Z.B. in einer 1/1000 Sekunde von einem weit entfernten Ort (im 3D-Raum), plötzlich in Sichtweite des Betrachter bewegt, DANN sieht der Betrachter doch zwangsläufig - Peng - eine Kugel die "einen Augenblick zuvor" noch nicht da war.

hier scheinst du nun endgültig eine Bewegung in Richtung der 4. Raumdimension mit einem Raumantrieb durcheinanderzuschmeißen.

Edit: jetzt dämmert's mir: du identifizierst eine Bewegung in Richtung der 4. Raumdimension mit der Bewegung durch ein Wurmloch in eine weit entfernte Region des Normalraumes. Und erliegst damit einem gewaltigen Denkfehler: eine Bewegung im Hyperraum senkrecht zum Normalraum muss ja nicht notwendigerweise etwas mit einem Wurmloch zu tun haben, und vor allen Dingen ist eine Reise durch ein Wurmloch auch gar keine Bewegung senkrecht zum Normalraum. Vielmehr wird der Normalraum so gekrümmt, dass sich ein Wurmlochtunnel bildet, und wenn man durch diesen hindurchfliegt, bleibt man voll und ganz im Normalraum, man bewegt sich nicht senkrecht zu diesem (wenn man sich das Wurmloch in einen Hyperraum eingebettet vorstellt). Der visuelle Effekt beim Eintritt in ein Wurmloch hat daher mit dem visuellen Effekt bei einer Bewegung in Richtung einer 4. Raumdimension überhaupt nichts zu tun.

Nun bewegt sich die Kugel (im Hyperraum) entlang einer Achse auf eine bestimmte Koordinate im 3D-Raum zu. Der Vorstellung wegen liegt diese Koordinate "auf der Grenze" der Raumzeit des 3D-Raumes:
http://666kb.com/i/b54ywg2qhtyvy3xol.png

du meinst, es bilde zwar der Normalraum mit der Zeit eine 4-dim Raumzeit, aber nicht der 4-dim. Hyperraum mit der Zeit eine 5-dim. Raumzeit? Dann musst du aber erstmal erklären, wie das funktionieren soll. Hier hast du ja zumindest das Wort "Zeit" eingezeichnet:

Stößt nun das Gebilde, von dem wir annehmen daß es eine Kugel ist, auf der "Zeit-Achse" mit dem 3D-Raum zusammen, so wird im 3D-Raum m.E. zuerst das sichtbar was "zuerst ankommt":

http://666kb.com/i/b54xzxsb8p05euro2.png

(schwarz=Hyperraum; rote Linie=Bewegungsrichtung auf einer Achse; gelb=Grenze zwischen Hyperraum und Raum-Zeit.)

aber leider nicht erklärt, was in dieser Grafik die Zeit sein soll. Ist vielleicht die Richtung der gelben Linie eine der Raumdimensionen und die Richtung der roten Linie vielleicht die Zeitdimension? Das wäre aber fatal: dann wäre ja die gelbe Linie der Rand der Raumzeit in zeitlicher Richtung, also der Urknall, der bekanntlich Mrd. von Jahren in der Vergangenheit liegt. Nach der Grafik existiert die Hyperkugel außerhalb unseres Universums, und könnte auch nicht mit diesem in Kontakt treten, der Kreis in der Grafik dringt ja nicht in den hellgrauen Bereich ein. Man müsste den Kreis in diesen hinein verschieben, dazu müsste Zeit vergehen, aber die Zeit ist ja schon als Koordinate auf der roten Linie berücksichtigt, man müsste also eine zweite Zeitdimension einführen. Das würde dann so aussehen, dass bei einigen Koordinaten auf der zweiten Zeitachse der Schnitt der Hyperkugel mit dem Normalraum nur in frühen Zeiten nach dem Urknall existierte und schon vor Jahrmilliarden verschwunden ist, während bei anderen Koordinaten der Schnitt heute noch vorhanden ist. Da wir aber auf der zweiten Zeitdimension eine feste Position hätten, da unser Empfinden einer voranschreitenden Zeit ein Wandern auf der ersten Zeitdimension (rote Linie) bedeutet, würde wir nur eine einzige dieser Varianten sehen können - eine Kugel, die im Laufe der Lebensdauer des Universums verschwindet.


.
EDIT (autom. Beitragszusammenführung) :
Agent Scullie schrieb nach 37 Minuten und 57 Sekunden:

Es ist ja nicht damit getan die Bindungsenergie des Planeten zu überwinden, sondern seine Masse wird ja zudem noch in Sekundenbruchteile auf eine relativ hohe Geschwindigkeit beschleunigt.

ich würde das mit der hohen Geschwindigkeit, mit der die Trümmerwolke von Alderaan auseinanderfliegt, nicht so genau nehmen, sondern als Show-Effekt einstufen, und mich damit begnügen, dass mit dem Aufbringen der Bindungsenergie die meisten Trümmer auch schon auf eine ordentliche Geschwindigkeit in der Größenordnung der Fluchtgeschwindigkeit (11,2 km/s) gebracht werden. Höhere Energien zu verschießen würde sich für das Imperium einfach nicht lohnen

[McWire]

darf ich fragen, wie du darauf kommst? Ich muss gestehen, ich habe nicht so wirklich verstanden, worüber ihr eigentlich am diskutieren seid, auch nach mehrmaligem Durchlesen eurer (deiner und McWire's) Postings nicht, aber soweit ich das mitbekommen habe, geht es ungefähr um folgendes: ihr stellt euch den Todesstern als 4-dim. Hyperkugel vor, diese existiert in einem 4-dim. Hyperraum, der sich aus den drei Dimensionen des Normalraumes und einer vierten Raumdimension zusammensetzt. Die Hyperkugel soll nun, während sie sich in Richtung der 4. Raumdimension bewegt, den 3-dim. Normalraum durchdringen, und ihr fragt euch, welchen visuellen Effekt das im 3D-Normalraum hat. Soweit richtig?

Aus meiner Perspektive hast du den Sacherverhalt richtig zusammengefasst. Zumindestens habe ich es so gemeint. Allerdings habe ich es nie auf den Todesstern bezogen, sondern allgemein auf ein beliebiges "Hyperraumobjekt durchdringt Normalraum"-Ereignis.

ich würde das mit der hohen Geschwindigkeit, mit der die Trümmerwolke von Alderaan auseinanderfliegt, nicht so genau nehmen, sondern als Show-Effekt einstufen, und mich damit begnügen, dass mit dem Aufbringen der Bindungsenergie die meisten Trümmer auch schon auf eine ordentliche Geschwindigkeit in der Größenordnung der Fluchtgeschwindigkeit (11,2 km/s) gebracht werden. Höhere Energien zu verschießen würde sich für das Imperium einfach nicht lohnen

Dank irgendeines verrückten Fans, der ein technisches Handbuch dazu geschrieben hat, sind die 10^38 Joule aber mittlerweile für das SW-Universum kanonisch (Frag mich aber bitt jetzt nicht welches Canon... irgendeins von den C-, G-, A-, B- oder sonstwas Canon )

Jedenfalls stellen die 10^38 Joule die allgemeine Diskussionsgrundlage zwischen mir, "Geforce" und "Darth Xanatos" dar... ich habe die einfach mal so akzeptiert.

Es ist nur eben jetzt das Problem, dass aufgrund der Schwerewirkung von Materie der Todesstern keine beliebige Masse und damit beliebige Dichte haben kann.

Ein guter Kompromiss zwischen Energieangabe und Fallbeschleunigung wäre wohl die Dichte von 500.000 kg/m³, was 20 mal so dicht wie das dichtest bekannte Element (Osmium) wäre.

Damit käme man für den größeren Todesstern auf eine Masse von ca 2,5*10^23 kg und damit auf eine oberflächliche Fallbeschleunigung von 82 m/s², was nicht ganz 8g entspricht.

Die Masse von 2,5*10^23 kg entsprechen eine Energieausbeute von 2,25*10^40 Joule, womit der Treibstoff bei einer durchschnittlichen Reaktor-Leistung von 10^32 Watt 7 Jahre reichen würde.

[General Quicksilver]

Diskussion zu Hypermatheriedichte/Lagerung/Hypergeometrie usw...

Ich habe mal nun dieses Thema ausgegliedert, weil, wie das schon mehrfach bemerkt wurde, das langsam wirklich extrem Off Topic wird.

_________________________________________________________________

Wie sieht es eigentlich mit meiner Idee des 4d-Lagertankes für 3D Matherie aus? ist die wirklich so sinnfrei, das da niemand drauf antworten möchte?