Zitat von Agent Scullie
Beitrag anzeigen
im eindimensionalen Fall nimmt die Gravitation gar nicht ab, sondern bleibt konstant,
die potentielle Energie nimmt man linear mit r zu.


die Definition der Energie. Energie ist Kraft mal Weg.





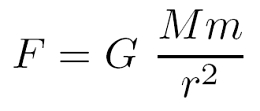




Kommentar